De “Dikke Barton” is voor mij één van de belangrijkste inspiratiebronnen voor hoe ik tegen mijn lessen aan kijk. Daarom korte beschrijvingen over hoe ik met het geleerde uit dit boek om ga.

Verdeelde-aandachteffect

Barton sluit aan bij de Cognitive Load Theory (CLT) Hij vertaalt deze theorie naar een aanpak die het geheugen van leerlingen zo min mogelijk belast. Vooral taken die niet essentieel zijn, neemt hij weg. In paragraaf 4.6 beschrijft hij het “verdeelde-aandacht-effect”. Met een aantal voorbeelden laat hij zien dat in veel situaties de informatie in wiskundeboeken dubbelop is. En dat belast het geheugen. Nou is het de CLT niet echt zonder controverse, maar dat het verstandig is om na te denken over waar je de denkkracht van leerlingen op wilt richten, staat buiten kijf. En wil je dat leerlingen bezig zijn om een tekening en een tekst te vergelijken, of wil je dat ze bezig zijn om het probleem dat voor ligt op te lossen? Met die blik is het gewoon ook gezond verstand.

Waar gaat het precies om? In het voorbeeld hieronder zie je een opgave uit Moderne Wiskunde (1984) waarin duidelijk wordt waar Barton het over heeft. In opgave 10 zijn de tekst en de informatie in de figuur dubbelop.

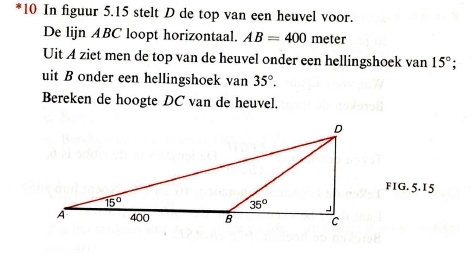
Barton stelt dan, dat dit de leerling verplicht om tekst en tekening met elkaar te vergelijken. Wellicht een nuttige actie bij andere vakken, maar niet bij wiskunde, aldus Barton. De opgaven die bij de actuele edities van Getal en Ruimte gebruikt worden in de onderbouw, hebben deze dubbeling ook. In het boek en in de opgavenbundels. Wanneer je naar oude eindexamen-opgaven kijkt, zie je dat de examensamenstellers enerzijds proberen de dubbeling te voorkomen, anderzijds de dubbeling (waarschijnlijk) gebruiken om extra aandacht op iets te vestigen.

Wat doe ik nu?

Eenvoudig. Ik haal de dubbelingen weg. Informatie waar de leerling mee aan de slag moet staat óf in de tekst, óf in het figuur / de tabel. Niet meer dubbel. Het is daarbij niet zo, dat ik het ene nooit meer gebruik en alleen nog maar het andere. Het wordt afgewisseld. De ene keer staat alles in een tekstje, de andere keer alles in het figuur. Maar niet meer dubbel. 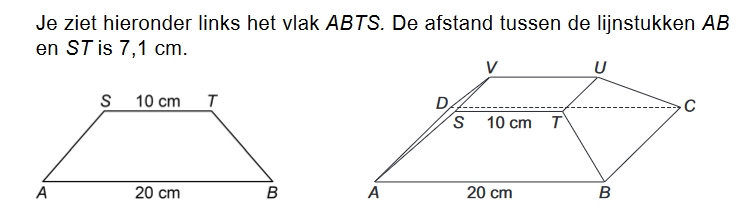Wat wel nog voor komt is dat sommige informatie niet in een figuur past. In de figuur hierboven (CSE VMBO-TL/GL 2021-1) zie je dit terug. De afstand tussen ST en AB wordt niet in de figuur gezet, omdat die dan onoverzichtelijk wordt. Of dat werkelijk zo is, lijkt mij dan een kwestie van smaak.

Ook kijk ik kritischer naar de opgaven. De opgave met de heuvel hierboven, is een soort redactiesom over een heuvel. Maar dat het om de hoogte van een heuvel gaat, is voor deze opgave overbodige ballast. De opdracht kan vereenvoudigd wat betreft presentatie, zonder de wiskundige waarde te veranderen, door af te sluiten met “Bereken BC”. Door dubbele en overbodige informatie weg te halen, worden opgaven minder leesoefeningen en zien we vooral de wiskundige capaciteiten van de leerling.

 

Barton, C. (2019). Volgens Barton: Lesgeven in wiskunde aan de hand van wetenschap, experts, en 12 jaar aan mislukkingen (R. Kneyber, Vert.; 1ste dr.). Phronese.
Jacobs, H. J., Kniep, W. J., & Krooshof, G. (1984). Moderne Wiskunde voor het voortgezet onderwijs: Vol. 5 voor havo en mavo (3de dr.). Wolters-Noordhoff.