Voortgangstoetsing in 3 VMBO-TL

Dit is een repost van een bericht geschreven juli 2004.

Een gewone wiskundemethode als “Moderne Wiskunde” nodigt uit tot een stramien van “hoofdstukje – proefwerkje”, net zolang tot het boek uit en het jaar afgelopen is. De wiskundedocenten van de School voor daltononderwijs Helen Parkhurst in Almere hebben in het schooljaar 2003-2004 in 3 vmbo–tl voortgangstoetsing ingevoerd. In dit artikel worden de achtergronden en de ervaringen hiermee besproken. Hierbij wordt uitgebreid aandacht besteed aan de statistische maat voor de kwaliteit van de toetsen.

Voortgangstoetsing

In het onderwijs toetsen we om te onderzoeken of datgene wat onderwezen is, ook echt geleerd is. De opbouw van schoolboeken met per hoofdstuk één onderwerp nodigt daarbij uit tot het toetsen per hoofdstuk. We veronderstellen dan dat wanneer alle stukjes beheerst worden, het totaal ook onder de knie is.

Voortgangstoetsing kijkt naar het einddoel, in dit geval het eindexamen. In dat eindexamen komen alle onderwerpen door elkaar en in samenhang aan bod. De voortgangstoetsen die gemaakt worden doen dat dus ook. In het ideale plaatje maken leerlingen steeds een toets op examenniveau, waarbij ze gaandeweg steeds beter scoren. Op de eerste toets wordt slecht gescoord, op de tweede beter, op de laatste wordt op examenniveau gescoord. Hierdoor krijgen leerlingen direct zicht op hoe het met de kennisontwikkeling staat en of examenniveau al bereikt is. Bij Helen Parkhurst in Almere is ervoor gekozen om per toets een gewoon schoolcijfer te geven, de cijfers op de voortgangstoets worden dus niet “vanzelf” beter. Leerlingen krijgen hierdoor niet direct zicht op hun kennisontwikkeling, maar wel op hun kennisniveau.

Waarover gaat de toets?

De voortgangstoetsen gaan over de tot dan behandelde stof uit het boek. De eerste toets gaat over de eerste twee hoofdstukken, de tweede over de eerste vier, enzovoorts. Welke specifieke onderwerpen in de voortgangstoets aan de orde komen is de leerlingen tevoren niet bekend. Meestal komen de meest recente hoofdstukken terug, maar welke oude hoofdstukken aan de orde is voor de leerlingen een verrassing. De keuze wordt gemaakt door de twee docenten die de toetsen samenstellen uit oude examenopgaven. Deze opgaven zijn op eindniveau en komen het dichtst bij wat er op het examen van de leerlingen gevraagd wordt. In één toets zitten ongeveer vier à vijf opgaven met ongeveer 18 items. Leerlingen zijn dan een vol lesuur van 70 minuten met de toets bezig. Om duidelijk te maken dat de toets over alle tot dan toe behandelde hoofdstukken gaat, wordt bij elke opgave vermeldt bij welk hoofdstuk dan wel paragraaf van een hoofdstuk de opgave hoort.

Ter illustratie zijn in Tabel 1 per toets de hoofdstuknummers uit Moderne Wiskunde, 7e editie, 3-vmbo-kgt opgenomen. De kolom onder “Hoofdstukken” geeft aan welke er aan de orde zouden kunnen komen, de kolom “Gedaan” geeft aan wat daadwerkelijk aan de orde is gekomen.

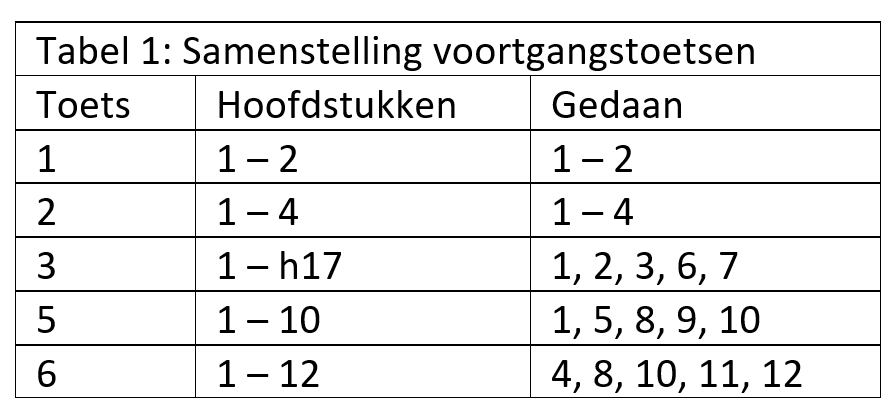
Duidelijk is dat naarmate het jaar vordert, bepaalde hoofdstukken regelmatig terugkomen zoals hoofdstuk 1 over grafieken, terwijl andere slechts incidenteel terugkomen zoals hoofdstuk 2 over plaatsbepalen.

De hoofdstukken die verwijzen naar algemene wiskundige vaardigheden, zoals het rekenen met procenten, het aflezen van coördinaten of de wetenschappelijke notatie, komen zelden expliciet aan de orde in eindexamenopgaven. Om ze wel terug te laten komen in de voortgangstoetsen worden hierover nieuwe opgaven gemaakt of worden bestaande opgaven uitgebreid.

Waarom voortgangstoetsing?

Voortgangstoetsing is ingevoerd om een aantal redenen. Allereerst blijkt bij het eindexamen steeds weer dat leerlingen slecht voorbereid zijn dan wel zich slecht voorbereid voelen, op het soort opgaven uit een eindexamen. Leerlingen ervaren een groot verschil tussen de gebruikelijke opgaven van een proefwerk en die zij op het examen moeten maken. Het verschil komt vooral tot uiting in de lengte van de opgaven, de hoeveelheid leeswerk en de complexiteit van de opgaven. De gewone proefwerkopgaven zijn te klein, hebben de te gebruiken informatie te expliciet opgenomen en gaan maar over één onderwerp.

Ten tweede ontbreekt er bij het stramien “hoofdstuk – proefwerk” voor leerlingen een direct belang om een slecht gemaakt hoofdstuk alsnog door te nemen. In 3TL is het examen zó ver weg… Met de voortgangstoets kan elk behandeld hoofdstuk terugkomen, wat een directe stimulans voor leerlingen is om hoofdstukken die geweest zijn toch te herhalen.

Derde reden is het verminderen van de hoeveelheid toetsing. Enerzijds omdat toetsing als zodanig teveel lessen kost, twaalf hoofdstukken in 3TL en zeven in 4TL kosten in het “hoofdstuk – proefwerk” stramien samen 19 lessen aan toetsing. Anderzijds omdat er met minder toetsen kan worden volstaan om te zien of leerlingen wiskunde geleerd hebben. In de drie trimesters van 3TL en de twee trimesters van 4TL worden in totaal 10 voortgangstoetsen afgenomen. Vergeleken met de 19 lessen in het oude stramien, blijven er dus negen lessen over die aan wiskunde besteed kunnen worden. De andere tijdsbesteding komt ook aan het einde van 4TL weer terug: het apart oefenen met oude examens is voor deze leerlingen niet meer nuttig. Ze hebben immers al heel veel examenopgaven gezien en geleerd hoe daar me om te gaan.

Laatste reden is dat ook docenten moeten leren om met examenopgaven en examen nakijkvoorschriften om te gaan. Op een grote school als Helen Parkhurst is zijn er elk jaar collega’s die 4TL voor de eerste keer doen.

Hoe gaan leerlingen er mee om?

De voortgangstoetsen zijn een onderdeel van de eisen die door de school aan leerlingen gesteld worden. In het PTA zijn voor wiskunde naast de voortgangstoetsen ook nog diagnostische toetsen per hoofdstuk als handelingsdeel opgenomen. Leerlingen maken deze diagnostische toetsen wanneer het hun uitkomt, Helen Parkhurst is tenslotte een Daltonschool waarin zelf plannen centraal staat. Een enkele leerling gebruikt de diagnostische toets als instap voor het hoofdstuk. Andere leerlingen gebruiken de diagnostische toetsen als afsluiting of als voorbereiding op de voortgangstoets. Nadat de diagnostische toets gemaakt is, kijken de leerlingen deze zelf na. In overleg met de docent wordt er dan een cijfer voor de diagnostische toets gegeven zodat leerlingen een beeld hebben van hun kennis en vaardigheid.

Voortgangstoetsing vraagt een andere voorbereiding door leerlingen. Dit is duidelijk te zien in de wijze waarop leerlingen de voortgangstoets benaderen. De eerste voortgangstoets wordt zonder al teveel problemen tegemoet gezien. Een toets over twee hoofdstukken, dat lukt wel. Na de toets is er uitgebreid commentaar op het type opgaven, de klachten die examenkandidaten normaal hebben, worden nu gehoord. De tweede voortgangstoets roept tevoren al vragen op: hoe bereid je een toets over vier hoofdstukken voor? Dit levert een aantal interessante klassengesprekken op. Hierbij wordt enerzijds stilgestaan bij de wijze van voorbereiden, maar ook bij de strategie die tijdens de toets gebruikt kan worden.

Latere klassengesprekken gaan in op de wijze waarop leerlingen zo’n toets maken. De strategie van “vooraan beginnen en doorploegen” blijkt voor een aantal leerlingen niet te werken. Met sommige onderwerpen hebben ze nou eenmaal minder affiniteit. Bij de tweede voortgangstoets blijken de leerlingen al een strategie te ontwikkelen die gericht is op het maken van de opgaven die punten opleveren, in plaats van de toets van voor naar achteren te maken.

Na de vierde voortgangstoets komen de meeste vragen over het lezen en aanpakken van de opgaven zelf.

Het feit dat er minder toetsen zijn, heeft ook invloed op de werkhouding van de leerlingen in de klas. Het stramien “hoofdstuk – proefwerk” gaf ook een ritme en zorgde vlak voor het proefwerk voor activiteiten bij leerlingen. Dat ritme is verdwenen. Met het ritme is ook de onrust aan het einde van een hoofdstuk verdwenen. Nog even snel het hoofdstuk doornemen omdat er een proefwerk aan komt is er niet meer bij. De voorbereiding op de voortgangstoets is toch meer een zaak van lange adem.

Proces van de voortgangstoets

De productie van één voortgangstoets kost ongeveer 10 uur. De start ligt bij het plannen van de toetsen in het trimester. Bij Helen Parkhurst geven zes docenten les aan 3TL, zij moeten vroegtijdig op de hoogte zijn van de periode waarin de toets afgenomen moet worden. Vervolgens wordt ongeveer één maand tevoren gekeken welke oude examenopgaven geschikt zouden zijn voor de toets. Op basis van de tot dan toe behandelde stof wordt een selectie gemaakt. Opgaven die ingaan op stof die de leerlingen nog niet kunnen, worden hierbij overgeslagen, immers, in 4TL wordt er nog steeds nieuwe stof onderwezen. Soms wordt een opgave met een aanwijzing of het geven van een antwoord, geschikt gemaakt voor de derde klas. Vervolgens worden deze opgaven overgezet naar de toets en worden de bijlagen gemaakt. Als laatste wordt bij de opgaven een nakijkvoorschrift en een puntentelling gemaakt.

Wanneer dit afgerond is, wordt het geheel rondgestuurd met het verzoek er de fouten uit te halen. De docenten verzorgen vervolgens zelf de vermenigvuldiging, de afname en de correctie. Na afname sturen de docenten hun scores per vraag in, op de wijze waarop dat bij het CSE ook dient te gebeuren. Wanneer van alle klassen de scores ontvangen zijn volgt een statistische analyse. Doel hiervan is om te bezien of onderdelen van de toets niet kloppen en om de omzetting van score naar cijfer te bepalen. Uiteindelijk ontvangen de docenten een formule waarmee ze voor hun leerlingen het cijfer kunnen bepalen. Daarna worden de cijfers aan de leerlingen meegedeeld.

Statistische verwerking

Zoals aangegeven wordt door één van de docenten de scores van de toetsen verzameld en vervolgens met SPSS^[1] verwerkt. Allereerst wordt de kwaliteit van de toets bekeken door middel van het beoordelen van de betrouwbaarheid van de opgaven en het beoordelen van de betrouwbaarheid van de hele toets. Wanneer dit afgerond is, wordt de normering vastgesteld.

Betrouwbaarheid van de opgaven

Een opgave in een toets heeft tot doel de kennis of vaardigheid van een leerling te meten. Goede leerlingen moeten de meeste opgaven goed maken, zwakke leerlingen alleen de eenvoudige opgaven. Of dat werkelijk zo is, kan gecontroleerd worden met een correlatiecoëfficiënt. Hiervoor wordt gekeken naar de zogenaamde item-totaal-correlatie (it-c). Een opgave met een positieve it-c wordt goed gemaakt door leerlingen met een hoge toetsscore en slecht gemaakt door leerlingen met een lage toetsscore. Een negatieve it-c geeft aan dat de opgave goed gemaakt wordt door zwakke leerlingen en fout door goede leerlingen. Wanneer dit het geval is, dient de opgave dus uit de toets verwijderd te worden.

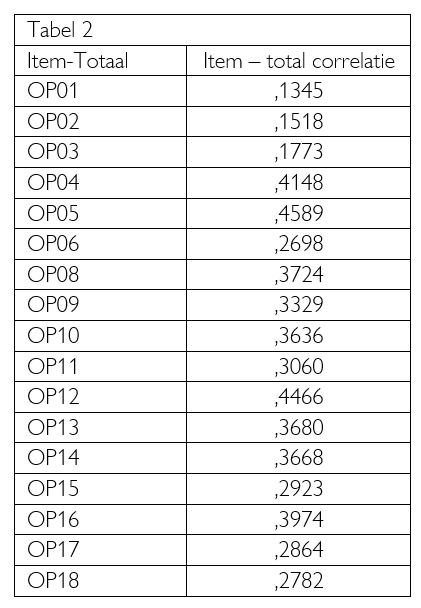
In Tabel 2 is een voorbeeld- uitdraai opgenomen. In de eerste kolom staan de opgaven aangegeven. De tweede kolom geeft de correlatie tussen de score op die opgave en de totaalscore voor de toets. Hierbij is gebruik gemaakt van de gegevens van één toets die door 120 leerlingen gemaakt is. Uit de tabel wordt duidelijk dat opgave 5 (op5) de hoogste correlatie met de toetsscore heeft. Leerlingen die die opgave goed hebben, hebben over het algemeen een hoge toetsscore en omgekeerd. De laagste correlaties worden gevonden bij de opgaven 1, 2 en 3.

Betrouwbaarheid van de toets.

Een voortgangstoets moet weergeven hoe het staat met de wiskundige kennis en vaardigheden van de leerlingen. De toets moet niet alleen onderscheid maken tussen goede en zwakke leerlingen, maar ook tussen goede en heel goede leerlingen. Een toets moet de gelegenheid geven om alle leerlingen in gedachten “op een rijtje” te zetten, de beste leerling links, de middenmoot in het midden, en de zwakke leerlingen rechts. Om dit te doen wordt dan gebruik gemaakt van de toetsscore. Hoge scores links, lage scores rechts enzovoorts. Belangrijk wordt dan of de toetsscores hiervoor geschikt zijn. Als maat hiervoor wordt gebruik gemaakt van Cronbach’s Alpha^[2] (zie kader). Een toets met een hoge Alpha heet dan betrouwbaarder te zijn dan een toets met een lage Alpha.

Voor toetsen in het reguliere onderwijs wordt een Alpha van 0,6 als acceptabel gezien. Een waarde van 0,8 is het maximum van wat praktisch haalbaar en wenselijk is^[3]. De Alpha neemt toe wanneer opgaven met een negatieve of lage it-c vervallen. Wanneer een opgave vervalt, verandert ook de totaalscore van de leerlingen op de toets. Stapsgewijs wordt dan ook gekeken naar een optimale combinatie van aantal opgaven, correlaties en Cronbach’s Alpha.

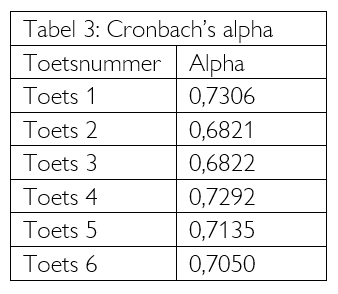
In Tabel 3 is ter illustratie de betrouwbaarheid per toets van de voortgangstoetsen uit het schooljaar 2003-04 opgenomen.

Bepaling voldoende / onvoldoende.

Wanneer duidelijk is dat de voortgangstoets als toets goed is, kan vervolgens uit de scores het cijfer bepaald worden. In het algemeen zijn er twee methodes om te bepalen wanneer een leerling een voldoende gehaald heeft, namelijk een absolute en een relatieve methode.

De absolute methode gaat uit van wat een leerling moet kunnen. Wanneer een leerling kan wat gevraagd wordt, bijvoorbeeld het foutloos maken van bepaalde opgaven, is er een voldoende behaald^[4]. De scores op andere opgaven zijn hierbij niet meer van belang. Een voorbeeld van deze manier van toetsen is het autorijexamen. Hierbij mogen bepaalde fouten niet voorkomen om te kunnen slagen. Bij deze manier van normbepaling kunnen extremen voorkomen: iedereen een voldoende dan wel een onvoldoende is mogelijk.

De relatieve methode gaat uit van wat leerlingen kunnen. Omdat er altijd zwakke leerlingen zijn, zullen er een aantal een onvoldoende krijgen. De hele goede leerlingen zijn net zoals de zwakke, relatief zeldzaam, een paar achten en negens kan, maar het blijft uitzondering (“een 10 is er alleen voor de meester”). De meeste cijfers worden dan gevonden rond de zes en de zeven: het resultaat van de grote middenmoot. Statistisch gezien behoren de scores van een toets normaal verdeeld te zijn en zijn de cijfers dat dus ook.

In de schoolpraktijk wordt meestal gebruik gemaakt van een combinatie. De meeste docenten hebben wel een idee van wat een leerling moet kunnen (absoluut), maar passen de normering aan wanneer er naar verhouding veel onvoldoendes vallen (relatief). Bijvoorbeeld omdat een proefwerk onbedoeld moeilijk was en er teveel onvoldoendes zijn^[5] (omgekeerd wordt merkwaardigerwijs door leerlingen en ouders niet geaccepteerd).

Bij het bepalen van de normering van deze voortgangstoetsen wordt alleen gebruik gemaakt van de relatieve methode. De scores van alle leerlingen (ongeveer 120) worden samengenomen. Daarna wordt er gezocht naar een formule waarmee een redelijk aantal leerlingen een voldoende cijfer krijgen. Als minimum wordt aangehouden dat ongeveer de helft van de leerlingen een cijfer boven de 5,5 moeten krijgen. Dit is in een grafiek weergegeven.

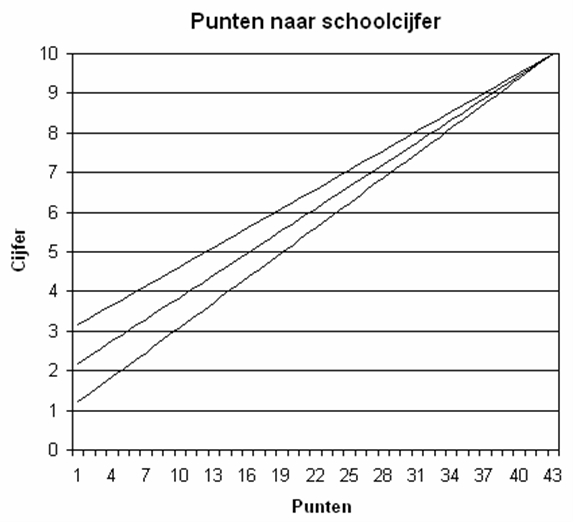
In de grafiek zijn drie lijnen opgenomen. De onderste lijn geeft de meest gebruikelijke omzetting van punten (in dit geval maximaal 43) naar schoolcijfer: 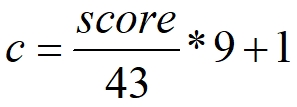Deze formule wordt als startpunt genomen. Wanneer deze formule meer dan de helft aan voldoendes oplevert, dan wordt deze formule gebruikt. Wanneer dit niet zo is, wordt de formule aangepast net zolang tot er voldoende leerlingen een voldoende cijfer hebben. Bij de bovenste lijn hoort een veel soepeler omrekening: 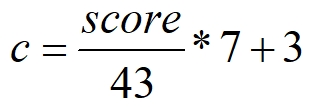Door het aanpassen van de formule op deze manier, stijgt vooral het cijfer bij de lage scores.

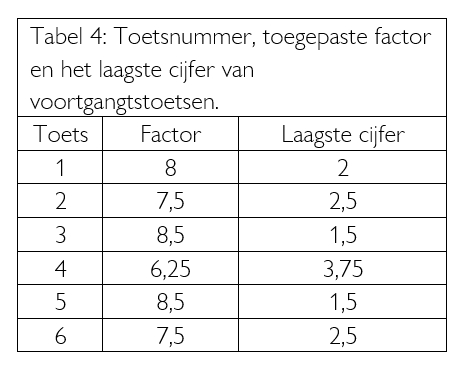
In Tabel 4 zijn ter illustratie de vermenigvuldigingsfactoren en het laagste te behalen cijfer opgenomen van de vier eerste voortgangstoetsen uit het schooljaar 2003-04.

Ervaringen tot nu toe

Van leerlingen

Leerlingen hebben duidelijk moeten wennen aan deze manier van toetsen. In de tweede klas wordt namelijk gewoon per hoofdstuk getoetst, de voortgangstoets is dus in ieder geval “anders”. En hij vraagt ook een andere manier van werken van de leerlingen. Allereerst vraagt de voortgangstoets in de voorbereiding meer zelfstandigheid en zelfdiscipline. De eerste toets over twee hoofdstukken, was voor velen nog wel te overzien, de toets over vier hoofdstukken gaf meer problemen bij de planning van de voorbereiding. Voorafgaand aan elke voortgangstoets is er dan ook expliciet stilgestaan bij de wijze waarop er voor de voortgangstoets geleerd kan worden.

Daarnaast liepen leerlingen er vanaf de eerste toets tegenaan dat ze meer na moeten denken over wat er nu eigenlijk gevraagd wordt. Voordat er aan de beantwoording van een opgave begonnen kan worden, moet nu eerst nagedacht worden waar de opgave wiskundig gezien over gaat: is het Pythagoras of is het tangens? Bij proefwerken per hoofdstuk hoeft een leerling zich dit meestal niet af te vragen.

Leerlingen maken de latere voortgangstoetsen niet meer op volgorde van de opgaven, maar zijn hun eigen weg gaan kiezen. Dus eerst de makkelijke opgaven, dan de opgaven met veel punten en als laatste de opgaven die moeilijk gevonden worden. Dit werd het meest duidelijk toen in één van de klassen een nieuwe leerling kwam: zij maakte de voortgangstoets opvallend slecht omdat ze teveel tijd besteed had aan een opgave die ze eigenlijk niet kon. Bij de daaropvolgende toetsen sloeg ze deze opgaven over en scoorde ze weer op haar niveau.

Dat de voortgangstoets over alle hoofdstukken gaat heeft in de loop van het jaar effect gehad op de werkhouding. Dat er vlak voor een proefwerk pas gewerkt wordt is langzaam verdwenen. Allereerst omdat duidelijk was dat de inhoud van de toets en het proefwerk waar aan gewerkt wordt niet automatisch bij elkaar horen. Daarnaast hebben de leerlingen ondervonden dat de latere voortgangstoetsen zo groot zijn dat het op het laatst aan het werk gaan weinig zin heeft.

Van collega’s

Ook voor collega’s is de voortgangstoets een verandering. De centrale verwerking was nieuw, en maakt het ook nog mogelijk om resultaten van collega’s en hun klassen onderling te vergelijken. Dat gaf bij sommigen een onprettig gevoel. Pas nadat er door alle betrokken docenten mee ingestemd was, zijn de resultaten van alle collega’s aan elkaar gepresenteerd.

Dat bij de normbepaling uitgegaan wordt van de leerlingen van zes klassen, heeft er één keer toe geleid dat één klas in zijn geheel onvoldoende scoorde, terwijl een andere klas in zijn geheel voldoende scoorde. Aangezien afgesproken was dat alle klassen dezelfde normering zouden hebben, konden de betrokken collega’s de normering niet aanpassen. Dat heeft bij de slecht presterende klas een vervelend lesuur opgeleverd, de docent had wel wat uit te leggen. Gelukkig bleek bij het bepalen van de trimestercijfers dat het gemiddelde met de andere voortgangstoets de slechte resultaten weer compenseerde. Uiteindelijk staan er bij alle leerlingen resultaten die passen bij het niveau van de leerlingen.

Bij de statistische analyse

De statistische analyse heeft een aantal zaken opgeleverd. Allereerst de vaste overtuiging dat de analyse plaats moet vinden met alle betrokken klassen. Het is aantrekkelijk om op basis van twee of drie klassen (van de zes), alvast een analyse te doen, opgaven te verwijderen en de norm te bepalen. Echter, elke klas extra geeft weer ongeveer 25 leerlingen erbij die de analyse toch beïnvloeden. Wanneer een zéér zwakke klas toegevoegd wordt, heeft dit wel degelijk effect op de normbepaling. Een extra klas beïnvloedt ook de betrouwbaarheid van de opgaven en de toets. Uit Tabel 3 komt naar voren dat de betrouwbaarheid van de toetsen bij meer dan 100 leerlingen prima is (Cronbach’s Alpha tussen de 0,6 en de 0,8). Dat terwijl er maar bij twee toetsen een enkele vraag verwijderd is. Dit komt vooral vanwege het grote aantal^[6] leerlingen dat de toets gemaakt heeft (rond de 120). Bij minder leerlingen, daalt de Alpha. Opgaven worden dan onterecht uit de toets verwijdert.

Het tweede dat opvalt, is dat er nogal wat “reparatie” plaatsvindt door middel van het aanpassen van de normering. Dat gebeurt omdat er vanuit gegaan wordt, dat het hier om “gewone” klassen gaat: niet slimmer of zwakker dan voorgaande jaren. Leerlingen uit deze klassen moeten dus over het algemeen een 6 of een 7 kunnen halen. Wanneer de toetscijfers dat in eerste instantie niet toelaten, dan ligt dat aan de toets en niet aan de leerlingen.

Dat er van zes klassen scores verzameld worden maakt onderling vergelijken mogelijk. De gevonden verschillen tussen klassen zijn meestal statistisch van belang en niet toe te schrijven aan toeval. De cijfers van de ene klas op de ene toets verschillen dus wezenlijk van de cijfers van een andere klas^[7]. In Figuur 2 is een boxplot weergeven van de cijfers van één voortgangstoets. Duidelijk zijn de verschillen tussen de tweede en de vijfde groep (klas). Geruststellend is de gedachte dat dit beeld per klas per toets wisselt.

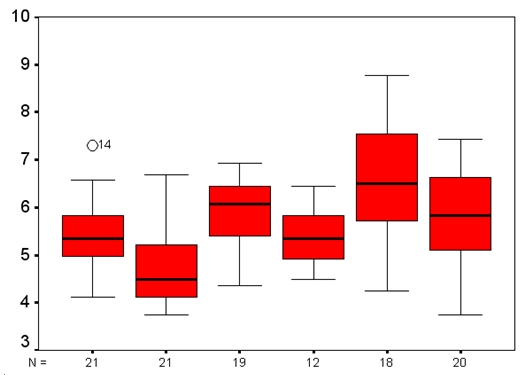
Uit de analyses blijkt ook dat de leerlingen van de docenten die de toets samenstellen, geen voordeel hebben.

Bij het samenstellen

Bij het samenstellen van de voortgangstoetsen zijn een aantal zaken naar voren gekomen. Allereerst het al eerder genoemde feit dat een aantal basisvaardigheden zoals het rekenen met procenten, schattend rekenen of het gebruik van de wetenschappelijke notatie in Moderne Wiskunde een apart hoofdstuk krijgen, terwijl ze – soms terecht – niet direct terugkomen in examenopgaven. Deze waarneming onderstreept dat wiskunde op het vmbo een hulpvak is voor andere vakken.

Daarnaast blijkt dat bepaalde zelfstandige onderwerpen, zoals kijkmeetkunde, in examenopgaven naar verhouding weinig terugkomen. Ook het onderscheid tussen de examenopgaven uit een jaar waarin informatieverwerking dan wel meetkunde centraal staat, is marginaal.

De keuze voor het gebruiken van examenopgaven blijkt grotendeels voor de kwaliteit van de voortgangstoetsen te zorgen. Uit de analyses blijkt steeds weer dat de zelf verzonnen opgaven de laagste it-c en een lage Alpha veroorzaken.

Dat eindexamenopgaven omvangrijk zijn, maakt dat er maar vier à vijf opgaven (met ongeveer 18 items), in één toets zitten. Het juist inschatten van de tijd die leerlingen hiervoor nodig hebben is dan nog een hele kunst en gaat nog wel eens mis.

Het foutloos samenstellen van een toets, bijlagen en een nakijkvoorschrift blijkt geen eenvoudige opgave. In elke toets hebben fouten gezeten. Het meest voorkomend zijn incorrecte verwijzingen naar afbeeldingen of bijlagen. Fouten in zelfgemaakte opgaven komen ook naar verhouding veel voor. “Even” een voortgangstoets maken, is er dus niet bij.

Reflectie

Over het invoeren van voortgangstoetsing is het docententeam aan het einde van het schooljaar 03-04 enthousiast. Meer tijd voor wiskunde, minder tijd aan toetsing tijdens de les, minder nakijkwerk, een andere manier van leren bij de leerlingen, het klinkt allemaal ideaal. Er zijn echter ook een kanttekening te maken. Wiskunde voor het vmbo gaat niet alleen over het maken van sommetjes en het doorgronden van theoretische wiskunde, maar gaat over het leren van kennis en vaardigheden die bij andere vakken of in het dagelijkse leven nodig zijn. Of voortgangstoetsing hierbij aansluit is nog maar de vraag.

Het doel dat leerlingen leren werken met eindexamenopgaven wordt gehaald: de 3e klas leerlingen hebben in zes voortgangstoetsen per toets vijf eindexamenopgaven gezien en gemaakt. Ze hebben ook hun manier van maken van opgaven kunnen aanpassen naar een voor eindexamenopgaven geschikte methode.

Dat stof steeds weer terugkomt zou een aanleiding moeten zijn om oude hoofdstukken te herhalen. Zonder aanwijzingen van de docenten blijkt dit niet te gebeuren. Onze 3TL leerlingen hebben nog niet de zelfsturing die hiervoor nodig is. Dat de voortgangstoetsen belangrijk zijn, is leerlingen duidelijk. Per trimester maar twee cijfers zorgt wel voor een serieuze benadering van de toetsen.

Door de voortgangstoetsen is wel de hoeveelheid toetsing en daarmee het nakijkwerk vermindert.

Reflectie (2)

(1 mei 2021)

Bijna 17 jaar later kijk ik deze blogpost terug. Ik vermoed, weet bijna zeker, dat wanneer ik contact zou opnemen met de wiskundesectie van de school, alleen de oudgedienden nog weten dat we dit gedaan hebben. Voorgangstoetsen worden niet meer afgenomen. Terug naar de toets-per-hoofdstuk. Het is verloren gegaan in de geschiedenis. Gedragen door een enkeling, gaan dit soort aanpakken verloren zodra de dragers verder gaan. Enerzijds is dat jammer, onderwijs, in dit geval toetsing, blijft op een bepaald niveau steken. Zo grondig als bij deze voortgangstoetsen wordt er zelden naar een gewone toets gekeken. Anderzijds logisch, waarom zou je committeren aan een toetssysteem dat een behoorlijke inspanning en een dito kennisbasis vereist, terwijl het materiaal van de uitgever, inclusief de toetsen, van redelijke kwaliteit zijn. En wellicht is er een geheel andere manier van toetsen ingevoerd. Iedere professional heeft het recht zijn eigen wiel uit te vinden.

Toetstechnisch begeeft deze aanpak zich in een turbulent water. Toetsen naar het examen toe, relatief normeren, enz, allemaal zaken die tegenwoordig met de nodige passie besproken worden. Toen ook, maar in een veel beperktere kring.

De opgedane kennis over deze toetsen, heeft mij zeker bescheidener gemaakt bij het beoordelen van klassen en leerlingen. Zo goed zijn de toetsen die dagelijks gebruikt worden niet. Alleen het grote aantal, maakt dat er een beeld uit komt dat wat zegt over wat de leerling kan wat betreft de schoolwiskunde. Het maakt dat wanneer er geroepen wordt dat er “teveel getoetst wordt”, ik op de rem ga staan. We toetsen, gelet op de kwaliteit van de methode-toetsen waarschijnlijk precies genoeg. Minder doet de leerlingen geen recht.

Toevoeging:

Cronbach’s Alpha

Een toets is een meetinstrument dat geijkt moet worden. Gebruikelijk is om bij ijking van een meetinstrument de waarden van dat instrument te vergelijken met een bekend meetinstrument. Zo is jarenlang de lengte van één meter vergeleken met de lengte van een standaardmeter opgeslagen bij de Technische Universiteit Delft. De eerste keer dat een eenheid geïntroduceerd wordt, is geen ijking mogelijk. Dan wordt gezocht naar externe omstandigheden om het meetinstrument mee “vast te leggen”. Denk bijvoorbeeld aan de schaal graden Celsius die loopt van het vriespunt tot en met het kookpunt van water. Wanneer ook dat niet mogelijk is, dan moet gekeken worden of het meetinstrument op verschillende momenten een vergelijkbare uitkomst geeft. Cronbach heeft hiervoor een formule ontwikkeld die dit doet.

Voordat we naar de formule gaan, is het nodig om duidelijk te hebben dat in de statistische wereld van Cronbach elk meetresultaat bestaat uit een echte score en een meetfout. En dan gaan we er ook nog vanuit dat we een meetinstrument hebben dat geschikt is voor ons doel.

Meetfouten zijn toevalligheden die het zicht op de echte score verdoezelen. Meetfouten zijn ook normaal verdeeld: meet ik de ene keer teveel, dan zal ik een volgende keer waarschijnlijk (!) te weinig meten. Naarmate de meetfouten kleiner zijn, en dat kan ik bijvoorbeeld zien aan de variantie, dan zit ik dichter bij de echte score. Die variantie speelt een centrale rol, ter herinnering de formule voor wat de variantie van een steekproef heet:

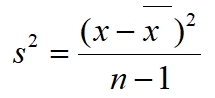
Hierbij is

• s² de variantie
• x de score van één leerling op één opgave
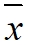• het gemiddelde van de leerlingen op die opgave
•  n het aantal leerlingen. Merk op dat dit aantal met 1 verminderd wordt.

De variantie is een kwadratische maat, grote afwijkingen van het gemiddelde beïnvloeden de variantie sterker dan kleine afwijkingen.

De coëfficiënt van Cronbach heeft de volgende formule:

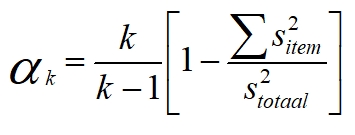
Hierbij staat:

• k voor het aantal opgaven
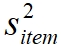• voor de variantie van één opgave, in de teller staat de som van de afzonderlijke varianties.
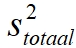• voor de variantie van de totaalscore.

Allereerst is duidelijk dat wanneer een toets langer wordt (k dus groter), het quotiënt naar 1 gaat. Hoe langer een toets, hoe beter. Dat is voor de hand liggend, naarmate ik met meer thermometers een temperatuur meet, zal de uitkomst betrouwbaarder worden. Het deel tussen de vierkante haken geeft aan dat wanneer de uitkomsten op de afzonderlijke opgaven, een lage variantie-som  hebben, ze beter meten wat er gemeten moet worden. En of een variantie naar verhouding laag of hoog is, wordt bepaald door de deling door .

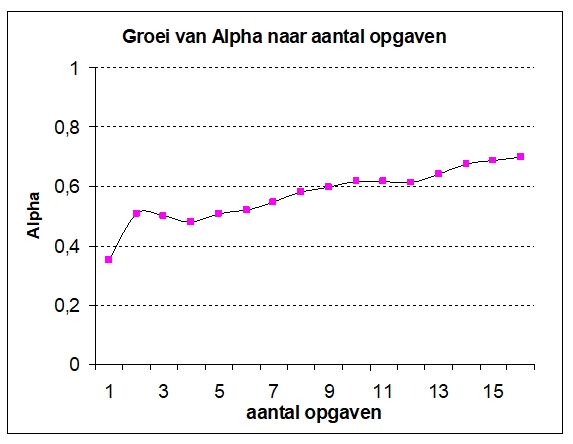
De Alpha is gevoelig voor het aantal opgaven waaruit de toets bestaat. Met het aantal opgaven neemt de som van de variaties per opgave toe. De term tussen de vierkante haken wordt dan steeds kleiner, terwijl ook naar 1 gaat. Hoe zich dat ontwikkeld is in Figuur 3 weergegeven. Daar is horizontaal het aantal opgaven uit de vierde voortgangstoets uitgezet, terwijl verticaal de Alpha staat. Duidelijk is dat de grafiek langzaam stijgt. Theoretisch is dan ook een lange toets beter dan een korte en zou een ideale kennismeting bestaan uit een zéér lange toets. Dat leerlingen vermoeid raken en daardoor meer fouten gaan maken, zorgt voor de genoemde grens van 0,8. Bij een toets is er dus altijd sprake van een afweging tussen betrouwbaarheid en praktische haalbaarheid.

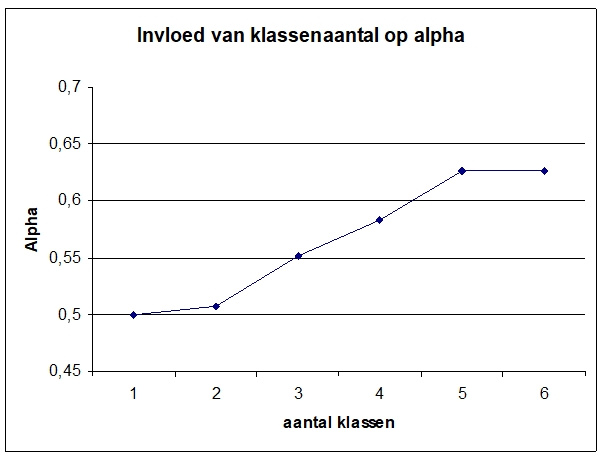
Ook het vergroten van het aantal leerlingen dat de toets maakt geeft een hogere Alpha. Dit vanwege de n in de formule voor variantie: Figuur 4 geeft de grafiek van de ontwikkeling van Alpha van de derde voortgangstoets naarmate er klassen toegevoegd worden. Tot vijf klassen stijgt de Alpha gestaag, de daaropvolgende klas geeft geen echte verandering meer. Nog een paar klassen toevoegen zal de Alpha niet wezenlijk doen veranderen.

Paul Ket is docent wiskunde en onderwijskundige. Twitter: @mathpaul

^[1] SPSS: Statistical Package for the Social Sciences.

^[2] Over Cronbach’s Alpha is veel geschreven. Zie o.a. Cronbach, L. J. (1990). Essentials of psychological testing (5th ed.). New York: Harper & Row. Een prima handboek met daarin de meestgebruikte statistische begrippen is van Slotboom, A. (1996). Statistiek in woorden een gebruikersvriendelijke beschrijving van de meest voorkomende statistische termen en technieken (2e dr. ed.). Groningen: Wolters-Noordhoff.

^[3] Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, N.J.: L. Erlbaum Associates.

^[4] Dit heet in onderwijskundig jargon “Criterion Referenced Testing”. Zie hiervoor bijvoorbeeld Ebel, R. L., & Frisbie, D. A. (1986). Essentials of educational measurement (4th ed.). Englewood Cliffs, N.J.: Prentice-Hall.

^[5] Deze praktijk is door A.D. de Groot in “Vijven en zessen” aan de kaak gesteld. Echter, omdat er nog geen voor de praktijk werkbaar alternatief is, blijft deze bestaan.

^[6] Er wordt in de statistiek over een “groot aantal” gesproken wanneer het toevoegen of verwijderen van een enkele leerling geen gevolgen heeft voor de gevonden waardes. Bij de Alpha van de voortgangstoetsen treedt dit op bij aantallen boven de 100.

^[7] Dat echte verschil leidt er toe, dat wanneer aan een onbekende leerling die een toets gemaakt heeft, het cijfer gevraagd wordt, op basis van dat cijfer de klas waar de leerling in zit genoemd kan worden.