Schema’s als samenvattingen: de concrete invulling van de studieaanwijzing.

Hoe leer je voor een proefwerk? Vaak wordt aan leerlingen de aanwijzing gegeven dat er een schema (woordweb) of samenvatting gemaakt moet worden. En je ziet leerlingen daar ook dapper mee aan het werk. Caviglioli (2019) stelt dat dit voor leerlingen alleen een effectieve strategie is wanneer zij op weg geholpen worden. Ik ben gaan kijken hoe dat er dan in mijn lespraktijk uit ziet.

Maak een schema

Menig werk over studievaardigheden geeft leerlingen als aanwijzing dat ze een schema moeten maken. Dat kan een woordweb, een begrippenlijst, een afbeelding, een hiërarchie of wat dan ook zijn, maar het moet een min of meer visuele weergave van de te bestuderen inhoud zijn. In zijn presentatie voor ResearchEdNL 2019 onderschrijft Caviglioli deze aanwijzing. Hij benadrukt zelfs het belang hiervan door de stellen dat elk onderwerp zich hier voor leent. Immers, of het nu over bomen, de Koude Oorlog of het oplossen van kwadratische vergelijkingen gaat, kennis is niet losstaand en heeft altijd verband met andere inhoud.

Hij stelt daar echter ook bij, dat het maken van een compleet, correct en relevant schema van de opsteller verlangt dat deze expert is. Alleen dan weet je de relatie tussen de verschillende onderdelen correct weer te geven. Een leerlingen of student is meestal nog geen expert en kan zo’n opdracht dan ook niet zelfstandig uitvoeren.

Leren voor de toets

Wanneer ik de aanwijzingen uit de cognitieve psychologie zoals die bijvoorbeeld door The Learning Scientist worden weergeven, volg, is één van de grote lijnen wel dat leerlingen actief iets moeten doen met de kennis. Of dat nu herhalen, tekenen of verwoorden is, het is een actie. Wanneer ik vraag wat leerlingen 1gym, 2havo en 2vwo werkelijk doen als voorbereiding voor een proefwerk, is dat meestal “de samenvatting doorlezen”. Een erkend ineffectieve aanpak. Maar welke alternatieven hebben ze? Nog meer sommen maken? Het gemaakte werk nog een keer doornemen? Weinig stimulerend of ook ineffectief.

Indachtig Caviglioli, heb ik leerlingen aan het einde van het hoofdstuk een schema gegeven waarmee ze het hoofdstuk konden doornemen.

Hieronder het schema dat ik voor de leerlingen 2h en 2v gemaakt heb over het hoofdstuk “Procenten en diagrammen” van de wiskundemethode Getal en Ruimte (12^e editie). Wanneer je van enige afstand naar het hoofdstuk kijkt, zie je dat het start met het rekenen met procenten als technische vaardigheid en dat er daarna een parade van diagrammen en centrummaten volgt. Voor een leerling een verzameling onderwerpen die niet direct veel samenhang vertonen.

Het schema laat dat ook zien. De vorm en de plaats van de tekstballonnen en -vakjes maakt duidelijk dat het over verschillende onderwerpen gaat, de bocht probeert duidelijk te maken dat er niet één duidelijke grote lijn is.
Onderop het papier staan nog een aantal vragen en aandachtspunten. De leerlingen krijgen vervolgens de opdracht om per vakje/ ballonnetje teksten, theorie, procedures, etc. etc. uit het hoofdstuk te vissen en het schema daarmee aan te vullen. Daar is dan geen “goed” of “fout” aan, het is een persoonlijk schema. Wel moeten de berekeningen, procedures die genoteerd zijn, wel kloppen. Misconcepties kunnen hiermee dus boven tafel komen.

In de les

Bij een drietal tweede klassen heb ik de tweede helft van het schooljaar (na de ResearchEdNL 2019) dergelijke schema’s uitgedeeld. De leerlingen kregen het schema op een vel A3 papier en ongeveer 50 minuten de tijd (bijna een hele les) om het schema naar eigen inzicht te maken. De enige eis van mij als docent was, dat ze het schema, eenmaal gemaakt, moesten fotograferen en digitaal moesten inleveren.

Opbrengsten

Onderstaand schema van een 2havo leerling. Het is redelijk beknopt en heeft ook het kopje “Spullen voor de toets” gekregen. Bij het ballonnetje “Diagrammen” staan wel de drie besproken diagrammen, maar hoe die gemaakt moeten worden, is niet opgenomen. Toch is dit voor een 2havo leerling een gebruikelijk schema. Het zoeken en vinden van informatie in het boek en dat opnemen in een schema vraagt daarbij dan ook veel sturing van mij als docent. Leerlingen doen dit niet “zomaar”, m.i. een teken dat ze er weinig ervaring mee hebben.

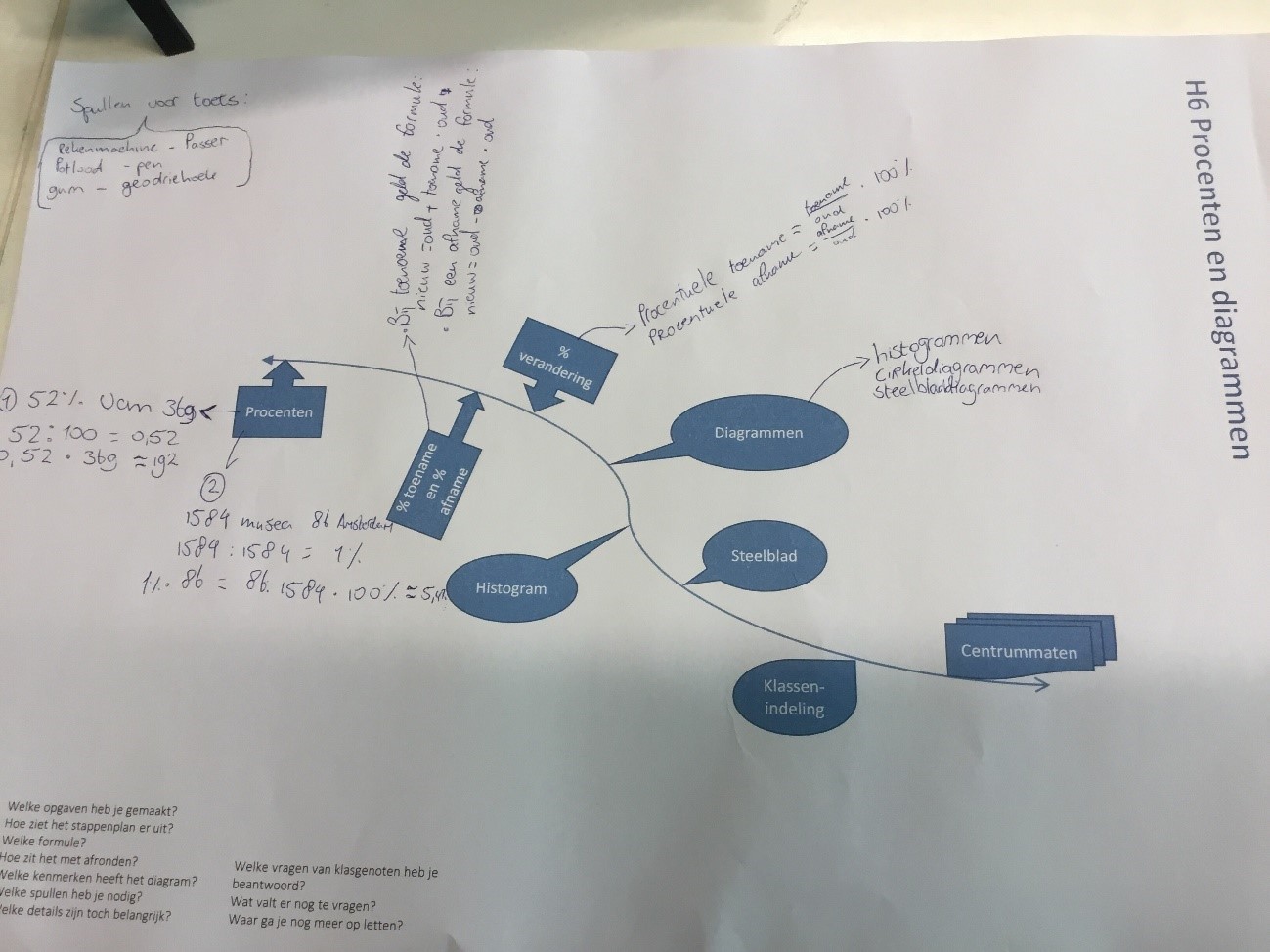
Na de eerste keer maken, waren de reacties overigens wel enthousiast. Vooral toen bij een aantal leerlingen bleek dat ze veel beter voorbereid waren (of voelden) en ook nog een beter resultaat hadden. Het resultaat, de intensiteit waarmee er aan gewerkt is, bleek geen indicatie voor het enthousiasme te zijn.

Onderstaande afbeelding met het werk van een 2vwo leerling laat een veel rijker voorbeeld zien van een aangevuld schema. Allereerst is duidelijk dat het laatste onderdeel, centrummaten, niet besproken is. Het is door de leerling doorgestreept. Dat heeft m.i. de voorkeur boven het onderwerp dat wel in het hoofdstuk zit niet in het schema opnemen. Doorstrepen is immers een actieve handeling. Daarna is door de leerlingen per onderwerp in het hoofdstuk beschreven wat er geleerd moet worden. Bij het ballonnetje diagrammen zijn de besproken diagrammen ook daadwerkelijk opgenomen en met een getallenvoorbeeld uitgewerkt.

Ook deze leerling was een enthousiast schema-maker en dichtte de hogere cijfers ook toe aan het aanvullen van het schema.

In 1gym worden de meest uitgebreide schema’s gemaakt. Dit schema is van hoofdstuk 5 van het 1gym boek Getal & Ruimte:

Opvallend is dan weer wel dat de check-list-vakjes onderaan de tweede pagina niet gebruikt worden.

Reacties

Ik heb nagelaten systematisch te informeren naar of en hoe de schema’s gebruikt zijn. Dat is iets voor het komende schooljaar. De eerste indrukken zijn dat:

• Het laat leerlingen zien waar in het hoofdstuk de accenten liggen die ik als docent gelegd heb.
• Leerlingen met een redelijk arsenaal aan studievaardigheden hebben de aanpak herkend als iets wat ze al doen en waarbij dit hen helpt.
• Leerlingen die normaal geen schema/woordweb o.i.d. maken, vinden het aanvullen van een dergelijk schema lastig.
• Leerlingen die zwak zijn in wiskunde, vinden het maken van dit soort schema’s lastig. Dat vraagt dus extra begeleiding.
• Leerlingen 2havo hebben meer begeleiding en sturing nodig om het schema op een goede manier aan te vullen. Goed in de zin van: als een bijdrage aan het repertoire studietechnieken en/of kloppend wat betreft de wiskunde die opgenomen wordt.
• De variëteit in de uitvoering is groot. Van min of meer leeg, tot geheel gevuld met meerder accentkleuren, tekeningen, cartoons, smileys en  vervolgaanwijzingen.

Twee leerlingen vroegen na de eerste keer expliciet naar het schema. Zij hadden op het proefwerk een voor hen opvallend hoog cijfer gehaald en legden het verband tussen het cijfer en het schema.

Hoe verder?

Waarnemingen die ik meeneem naar volgende schooljaren:

• Het maken van een dergelijk schema is voor een docent een klusje, maar eenmaal gemaakt kan het een aantal jaren mee. Dat het ene jaar het accent anders ligt dan het andere jaar, is een reden om actief het schema aan te passen, en dat past helemaal in de aanpak.
• De schema’s blijven voor leerlingen alleen beschikbaar op papier en niet digitaal, zodat het schrijven en tekenen onderdeel wordt van de verwerking van de stof.
• Leerlingen krijgen aan de hand van voorbeelden zicht op de bedoeling van het schema. Zonder voorbeeld is het een weinig concrete opdracht die teleurstellende resultaten heeft.
• Begeleiding is maatwerk.
• Het lijkt mij zaak om leerlingen met een ineffectieve manier van studeren te stimuleren of zelfs te dwingen, het te gaan gebruiken. Anderzijds kan het al dan niet gebruiken van zo’n schema ook een invulling van meer maatwerk op school zijn: niet iedere leerling heeft zo’n studiehulp nodig.

Bestanden

Hieronder vind je de bestanden van de schema’s bij de verschillende hoofdstukken.